Attention is all you need - 전설의 논문을 온전히 흡수하는 방법
약 8년 늦은 리뷰?
나름 데이터 분석과 머신러닝을 공부하고 실무에 사용하고 있지만, 정작 현재 AI 기술을 이끌고 있는 트랜스포머에 대해서는 교양 수준으로 이따금씩 전해 들은(그리고 곧 까먹은) 것이 전부라 늘 아쉬웠습니다. 딥러닝 쪽 신기술을 실무로 제대로 사용해 본 경험이 많지 않아 비교적 최신 개념인 트랜스포머가 낯설기도 했고, 트랜스포머를 온전히 이해하기 위해서 먼저 알아야 하는 선수 지식이 생각보다 많기 때문이기도 했습니다.
그래서 몇 주간 딥러닝 기초, pytorch, NLP 기초, RNN, LSTM, seq2seq, attention 등의 선수 개념을 익히고, 트랜스포머를 설명한 다양한 블로그 글과 유튜브 클립을 보며 트랜스포머를 이 세상에 처음 소개한 전설의 논문, “Attention is all you need(2017)”의 원문을 비로소 읽고 분석할 수 있었습니다.
이 트랜스포머 논문을 꼼꼼히 읽고 이해한 과정을 시각화 하고, 코드 단위로 직접 구현해보며 이번 달의 블로그 포스트로 기록하고 싶었지만, 금세 한가지 문제를 마주쳤습니다. 이 논문 리뷰나 해설을 하는 글을 쓰기엔 약 8년 정도 늦었다는 것입니다… 😅
이 글을 쓰는 2024년 시점에서 트랜스포머 자체는 딥러닝을 전공하시는 분들께는 이미 상식 수준으로 받아들여지고 있고, 이 논문을 리뷰한 블로그 글은 지난 8년 동안 수도 없이 쌓여 있습니다. 다음 영역에서 소개하겠지만, 트랜스포머의 구조나 원리를 세상에서 가장 훌륭하게 시각화한 자료들을 두고 이를 제가 유사하게 다시 하는 것은 큰 의미가 없을 것이라고 생각했습니다.
그렇기에 이 글은 두 가지 차원에서 이 원조 트랜스포머 맛집(?) 원문을 주제로 유의미한 정보를 담으려고 합니다.
첫째, 트랜스포머나 생성 AI 관련 공부를 시작하고 싶은데 미리 알아야 하는 개념이 너무 많아 막막한 분들께 일종의 로드맵을 제공하는 글이 되었으면 합니다. 트랜스포머 (특히 원조 트랜스포머)를 온전히 이해하기 위해 알아야 하는 핵심 선수 개념과 그것을 제가 가장 효과적으로 이해한 자료들을 소개하며 학습에 도움이 되었으면 좋겠습니다.
둘째, 이 논문을 파헤치면서 들었던 개인적인 의문점과 테크니컬한 고민을 FAQ 형식으로 나열해 이 논문을 직접 읽으시면서 저와 비슷한 의문을 가진 분들에게 트랜스포머에 대한 더 깊은 이해를 제공하고자 합니다.
이 글을 온전히 즐기기 위해 필요한 것들
이 글의 다음 영역인 “Attention is all you need - FAQ” 영역을 온전히 이해하고 각 질문에 공감하기 위해서는 지금까지의 제 어떤 블로그 글보다 요구되는 선수 지식이 많습니다. 논문 원문을 처음부터 끝까지 읽어보고 어느 정도 이해한 상태에서 시작을 해야하니까요. 정확하게는, 트랜스포머를 이해하기 위한 모든 지식을 가진 상태에서 이 논문을 읽어야 큰 막힘 없이 논문의 핵심 아이디어를 공감하며 읽어 나갈 수 있습니다.
저도 아직 100% 이 논문을 이해했다고 할 수는 없지만, 수많은 웹사이트와 공식 문서, 유튜브 영상을 찾아보며 제가 아무 것도 모르던 상태에서 어떻게 현재 수준으로 이해도를 올렸는지를 역추적 했습니다. 그리고 나열한 것이 이 영역에서 추천드리는 자료들입니다. 너무 유명한 자료도 많고, 그렇게 유명하지 않은 자료도 있지만 모두 각 개념에 대한 기본 개념을 잘 잡아주거나 흔히 빠질 수 있는 오개념을 바로 잡아주는 유용한 자료들이었습니다. 최대한 중복되는 개념이 없도록 제가 봤던 모든 자료를 넣은 것이 아니라 해당 개념을 가장 잘 설명했던 자료만 골랐습니다.
여기에서 소개된 자료 외에 여러분이 딥러닝 분야를 공부하면서 참고한 좋은 자료도 다른 분들을 위해 언제든지 댓글로 남겨주세요!
여기서의 로드맵은 파이썬 문법 및 머신러닝의 기본 셋업 (모델, 학습, 추론 등)은 충분히 이해하고 있다는 전제하에 딥러닝 쪽 지식을 쌓아올리는 방법을 소개합니다.
딥러닝 기초
가장 먼저 알아야 할 개념은 전통적 머신러닝이 아닌 딥러닝의 핵심 셋업과 학습 및 추론 방법론입니다. 더 구체적으로는 바닐라 딥러닝 네트워크, MLP, feed-forward network, fully connected layer 등의 이름으로 불리는 가장 기본적인 형태의 딥러닝 네트워크에 대한 다음 개념을 제대로 이해하고 설명할 수 있는 수준이 되어야 합니다.
Multi layer perceptron, activation function, forward propagation, minibatch training, loss function, backpropagation, computational graph, optimizer, learning rate scheduler, batch normalization, dropout, hyperparameter optimization
제가 이러한 개념을 학습한 자료는 다음과 같습니다.
- 밑바닥부터 시작하는 딥러닝 (사이토 고키 저): 말 그대로 딥러닝을 밑바닥부터 설명하는 책입니다. 이 영역에서 유일하게 무료로 볼 수 없는 책의 형태이기 때문에, 이 책을 사기 싫으시다면 유명한 Stanford CS231n 수업을 들으셔도 무방합니다. 이 책에서도 CS231n 수업의 많은 부분을 참고 했다고 했으며, 특히나 계산 그래프(computational graph)를 통해 딥러닝 네트워크의 역전파 과정을 밑바닥부터 알려주는 챕터는 흔히 블랙박스나 하이 레벨로만 알고 있는 역전파 과정을 조금의 모호함의 여지도 없이 낱낱히 파헤쳐 정말 유익했습니다.
- Youtube 3Blue1Brown Neural Network Series #1~#4: 수학이나 통계 쪽 시각화의 권위자인 3Blue1Brown 채널이 딥러닝 네트워크에 관해 남긴 시리즈입니다. 그 중에서 첫 4개의 영상은 기본 딥러닝 네트워크의 추론과 학습 과정을 직관적으로 시각화해 딥러닝이 이토록 쉬운 개념이었는지 착각이 들게 할 정도입니다. 또한 생각보다 각 영상의 밀도가 높아 이 시리즈를 여러 번 볼때마다 이전 시청에서는 놓쳤던 새로운 인사이트를 추가할 수 있습니다.
- Youtube StatQuest Neural Networks/Deep Learning Series #처음~#Part 7: StatQuest 역시 머신러닝 및 통계 관련 시각화 권위자로, 원래는 머신러닝 쪽 영상만 만들다가 딥러닝 쪽 영상을 3년 전부터 만들기 시작해 지금까지도 계속 추가되고 있습니다. 그 중 deep learning 시리즈의 시작부터 Part7 (cross entropy and backpropagation) 정도가 딥러닝의 기본을 익힐 수 있는 영역입니다. StatQuest는 어떤 어려운 개념을 설명하든 숫자 단위로 예시를 단순화 해 설명하는 특징이 있어 대충 “미분을 해서~” 또는 “행렬을 ~ 연산을 해서”와 같이 직접 숫자 단위로 계산을 보여주지 않고 넘기는 일이 없습니다. 그렇기에 모든 연산을 하나하나 따라가며 개념을 익힐 수 있으며, 저처럼 수식보다는 예시를 통한 이해를 선호하시는 분들께 인기가 많은 것 같습니다. 딥러닝 영상에서도 단순화한 예시를 통해 각 레이어가 왜 필요한지, 복잡한 데이터 분포를 딥러닝의 파라미터들이 어떻게 따라갈 수 있는지 등의 유익한 인사이트를 얻을 수 있습니다. 영상의 예시나 노래, 분위기는 중학교 수학을 설명하는 것처럼 단순해 보여 처음에는 이질감이 들 수 있으나, 대학 과정의 통계 및 머신러닝 개념을 중학생도 이해할 수 있게 설명한다는 점에서 이 고인물 (생물통계학 교수님이라고 합니다) 의 무시무시한 능력을 엿볼 수 있습니다.
Pytorch
- Pytorch 공식 문서 “Introduction to PyTorch”, “Introduction to PyTorch on YouTube”: 위의 과정을 통해 딥러닝의 수학적 원리와 개념을 익혔지만, 그것을 코드로 옮기는 것은 또 다른 일입니다. 이를 위해 여러 자료를 찾아 보았지만, 공식 파이토치의 문서들을 정주행 하는 것보다 효율적인 자료는 찾지 못한 것 같습니다. 딥러닝의 학습/추론 단계에서 forward propagation, backward propagation이 어떻게 이루어지는지, 그 과정을 통해 얻은 그레이언트는 어떻게 각 파라미터에게 전달이 되는지 등을 코드 단위로 익히다보면 딥러닝에 대한 더 단단한 개념이 잡히는 것 같습니다. 또한 대부분의 예시에서 인풋이 고정된 사이지의 이미지인 경우가 많아 조금 더 나간다면 CNN 계열의 모델 구조도 익힐 수 있어 좋습니다.
RNN~Transformer
이제 기본적인 딥러닝 메커니즘에 대한 이론적 이해와 코드 구현이 자리 잡았다면, RNN 부터 시작하는 가변 길이 인풋 (주로 자연어)을 다루는 딥러닝 기법의 역사를 따라갈 차례입니다.
- Youtube StatQuest Neural Networks/Deep Learning Series #RNN~#Attention: StatQuest에 대한 칭찬은 위에서도 했으니 여기서는 생략하겠습니다. 위와 동일한 재생목록을 따라가다보면, RNN 부터 시작해 LSTM, word embedding, seq2seq, attention에 이르기 까지의 연구자들의 고민과 아이디어를 엿볼 수 있습니다. StatQuest 특유의 뛰어난 강의력 덕분에 이해가 잘 되는 것은 물론이지만, 각 개념을 살펴보면서 “여기서 이 연산을 왜 저렇게 할까?”, “여기서 이렇게 하면 무엇이 잘 안되지 않나?” 와 같은 질문을 던지면서 갈수록 각 개념과 더 발전된 다음 개념의 동기 또한 더 잘 받아들 일 수 있습니다. StatQuest 또한 모든 내용을 온전히 이해하기 위해 n회 정주행을 권장합니다.
Transformer
이제 트랜스포머 자체에 대한 자료를 소개할 차례입니다.
- Youtube StatQuest Neural Networks/Deep Learning Series #Transformer~(현재 진행형): 이제 transfomer와 그 여러 가지 변형, decoder-only transfomer, query key value 행렬 연산을 직접적으로 다루는 영상들입니다. 트랜스포머가 실제로 기존의 모델 구조와 다른 점이 많아 그 차이점 (recurrent 또는 convolutional layer 없이 self-attention layer만을 이용, 가변 길이의 인풋을 가지고 어떻게 병렬화를 진행하는지 등)에 주목해 보면 좋습니다.
- Youtube 3Blue1Brown Neural Network Series #5~(현재진행형): 4화까지가 기본 딥러닝에 대한 완결된 시리즈이었다면, 어떤 연유에서인지 3Blue1Brown이 최근 GPT를 설명하기 위한 영상을 새로 올려 적잖게 놀랐습니다. 영상은 GPT와 같은 decoder only transformer를 다루고 있으며, 실제 GPT-3의 구조를 있는 그대로 설명해 전반적인 규모를 파악하기 좋습니다. 예시를 단순화해 숫자 단위로 연산을 보여주는 StatQuest와, 실제 규모를 추적하며 설명하는 3Blue1Brown의 설명 형식이 상호 보완하며 더 깊은 이해를 할 수 있습니다.
- “The illustrated transformer” Jay Alammar blog post: 유명한 딥러닝 연구자 및 교육자인 Jay Alammar 교수님의 “the illustrated transformer”를 보며 실제 “Attention is all you need” 논문을 한 번 읽은 것 같은 효과를 누릴 수 있습니다. 이 포스트는 먼저 읽기보단 “Attention is all you need” 원문을 읽다가 이해가 되지 않는 영역을 시각화하고 싶을 때 함께 보면 더욱 좋은 것 같습니다.
- Youtube “How a Transformer works at inference vs training time”: 아마 지금까지 나온 자료 중 가장 유명하지 않은 자료이지만, 트랜스포머에 대한 제 이해를 키워준 정말 중요한 자료입니다. Hugging Face에서 AI Engineer로 근무하고 있는 분의 영상이며, 트랜스포머가 학습 시간과 추론 시간에 정확히 어떻게 작동하는지를 세세히 풀어 설명하는 영상입니다. StatQuest나 3Blue1Brown의 영상에서는 주로 트랜스포머의 추론 시간에 초점을 맞춰 설명해 정확히 트랜스포머가 학습 시간과 추론 시간에 어떻게 다른지, 각 단계에서 query key value 연산을 어떻게 병렬화하는지 헷갈렸는데, 이 영상 하나를 통해 의문을 해소할 수 있었습니다. 또한 Hugging Face의 API와 code convention에 대한 내용도 익힐 수 있어 좋았습니다.
여기까지 왔다면 별도의 검색이나 노력 없이도 “Attention is all you need” 원문을 수긍하며 읽어나갈 수 있습니다!
Attention is all you need - FAQ
이 영역에서는 제가 “Attention is all you need” 논문을 읽으며 들었던 궁금증과, 각 궁금증에 대한 제 답변입니다. 각 아이디어에 대한 더 깊은 이해를 하고자 작성했으며, 이미 논문을 읽으신 분들이 보시면 더욱 좋을 것 같습니다.
\[Attention(Q, K, V) = softmax(\dfrac{QK^t}{\sqrt{d_k}})V\]수상하게 $\sqrt{d_k}$로 나누는 이유?
Transformer attention의 본질을 담고 있는 수식입니다. Query, key의 유사도로 value를 가중합 하는 아이디어를 이해한 후 가장 처음 드는 의문은, 저 수상한 $\sqrt{d_k}$의 정체입니다. 원문의 저자들은 “pushing the softmax function into regions where it has extremely small gradients”이라고 설명하는데, 이게 조금 더 구체적으로 무엇을 의미하는지가 궁금했습니다. 직관적으로 어느 하나의 (query, key) 쌍의 유사도가 압도적으로 높다면 그 조합을 제외한 softmax의 결과는 0.0에 가까워 질 것이고, 이는 여러 value의 선형 결합보다는 일방적으로 가장 유사도가 높은 단 하나의 value만 쓰일 것이기에 $d_k$가 커질수록 이러한 점이 학습에 방해가 될 것이라고 생각했습니다. 하지만 “gradient”라는 말을 사용한 것을 보면 이것이 softmax의 backpropagation과 연관이 있다고 생각해 알아보았습니다. 결국 softmax의 backprop의 특성 상 이렇게 단 하나의 조합에 압도적인 최대값이 존재할 수록 backprop 시 gradient가 0.0에 가까워지는 문제가 발생해 vanishing gradient 문제와 유사한 문제가 일어남을 알게 되었습니다. 이 문제와 연관된 softmax의 정확한 backprop 식에 관한 내용은 이 글에서 확인할 수 있었습니다.
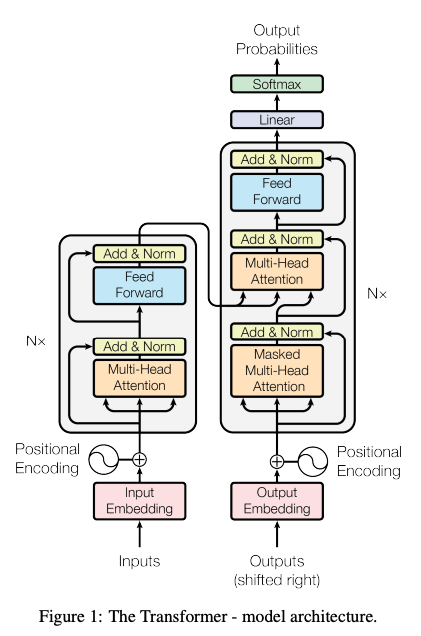
Outputs (shifted right)의 의미?
이 유명한 그림 속 오른쪽 아래의 Outputs (shifted right)의 의미가 궁금했습니다. 이는 트랜스포머 뿐만 아니라 전반적인 가변 길이 input 가변 길이 output 모델에서 자주 사용되는 셋업으로, 디코딩 시 바로 전 단어들까지를 보고 바로 다음 단어를 맞추는 세팅에서 유래합니다. 처음 디코딩을 시작할 때는 이전의 output이 없기 때문에, SOS (start of sentence) 토큰을 decoder의 인풋 삼아 첫 아웃풋 토큰을 생성하고, SOS 토큰과 첫 아웃풋 토큰을 인풋 삼아 다음 추론을 진행하고, 하는 식으로 추론이 진행됩니다. 이는 학습 시간에도 마찬가지인데, decoder의 아웃풋이 하나하나 생성될 때까지 기다렸다가 그것을 다시 인풋을 넣는 추론과 달리, 학습 시간에는 이미 아는 정답 토큰들을 SOS 토큰을 포함해 하나씩 오른쪽으로 밀어서 (shifted right) 통째로 decoder에 넣어 loss를 계산하는 식으로 진행이 됩니다. 즉 가변길이 인풋 아웃풋 모델의 특성상 SOS 토큰을 디코더의 인풋으로 포함되어야 하기 때문에 “shifted right”이라는 표현이 자주 쓰입니다.
인코더에서는 모르지만 디코더에서는 이전 단계 디코더의 아웃풋이 다시 디코더에 인풋으로 들어가기 때문에 이전 디코더의 결과를 기다려야 하는데, 어떻게 Q, K, V 연산을 병렬화 할 수 있는가?
대부분의 트랜스포머 설명 자료에서는 chat GPT와 같은 decoder only transformer를 다루기 때문에 추론 시간에 집중해서 설명을 하는 경향이 있습니다. 이 질문도 트랜스포머의 추론 시간과 학습 시간의 셋업이 어떻게 다른지 몰라서 생긴 궁금증이었습니다. 트랜스포머의 가장 큰 장점 중 하나가 기존에 recurrent한 네트워크가 필요하다고 알려진 NLP 분야에서 GPU를 사용한 병렬화 연산을 최대한 활용할 수 있는 능력인데, 디코더 단에서 이전 단계의 추론 결과를 매번 기다려야 한다면 병렬화의 의미가 조금 퇴색되지 않을까하는 궁금증이었습니다. 이 궁금증은 위에서 언급한 트랜스포머의 추론과 학습 시간의 차이를 다룬 영상을 통해서 해결되었습니다.
추론 시간에는 위에서 살펴보았듯이 디코더에서 바로 이전 단계의 결과가 다음 단계 디코더의 인풋으로 들어가기 때문에 sequential한 연산이 필요하지만, 이는 추론 단계라 시간이나 자원이 많이 소요되지 않아 크게 병렬화가 진행되지 않아도 학습에 비해 성능에 큰 타격이 없습니다. 반면 학습 시에는 인코더에 모든 인풋 토큰과 디코더에 right shift 된 정답 토큰들이 모두 마련되어 있고 실제 인코더와 디코더는 하나의 인풋에 대해 한 번만 forward/backward pass를 하면 되기 때문에 단어 하나하나의 추론을 기다리지 않고 병렬 연산을 진행할 수 있습니다. 학습시 디코더의 결과 (아마 정답과는 다른)와 무관하게 디코더의 인풋으로 right shift 된 정답 토큰들을 넣어주는 것을 “teacher forcing”이라고도 합니다.
인코더와 디코더에 가변 길이의 인풋이 들어오면 self-attention 연산 구조나 할당 받아야 하는 메모리 크기가 늘 달라질텐데, 병렬화나 메모리 최적화를 제대로 진행할 수 있는가?
트랜스포머의 학습/추론 시간의 동작을 확인한 후 그 다음 들었던 생각은 “I am a student”와 같은 짧은 인풋 문장을 받을 때와 몇백 단어가 넘어가는 문단을 인풋을 받을 때 병렬화와 메모리 할당 최적화를 제대로 수행할 수 있는지 였습니다. 상식적으로 생각해도 짧은 문장과 긴 문장이 들어올때마다 O(n^2)로 바뀌는 메모리와 시간이 병렬화에 유리하지 않아보였기 때문입니다. 그렇기 때문에 실제 구현된 트랜스포머는 일정 길이의 max context length (인풋 토큰의 길이)를 설정해두고, 그것보다 짧은 문장을 받아 남은 부분은 padding으로 채우는 전략을 취합니다. 이를 통해 트랜스포머 모델은 늘 어느 정도 일정한 수준의 메모리와 연산 자원을 가지고 학습을 진행할 수 있습니다.
인코더-디코더 attention에서 encoder에서의 sequence size와 decoder의 sequence size가 같아야 하는가?
트랜스포머의 self-attention을 설명하는 대부분의 자료에서 Q, K, V의 sequence size를 같다고 생각하고 설명을 전개하는 경우가 많은데, 이는 실제로 인코더의 self-attention과 디코더만의 masked self-attention에서는 대부분 해당되는 이야기입니다. 하지만 encoder-decoder attention이 진행될 때는 가변길이 모델의 특성상 인코더 쪽의 sequence size와 디코더 쪽의 sequence size가 같지 않는 경우가 있을 것입니다. 하지만 이런 경우에도 attention 메커니즘은 정상적으로 작동합니다. 인코더 쪽에서 K, V를 가져오고 디코더 쪽에서 Q를 가져오니 행렬 차원만 놓고 보았을 때는 다음과 같은 행렬곱이 이루어집니다. 편의를 위해 $\sqrt{d_k}$로 scaling 하는 것은 생략했습니다. 또한 이 논문에서의 $d_{model}=512$ 값을 사용하겠습니다.
\[K: (n,512), Q: (m, 512), V: (n, 512)\] \[QK^t: (m,n)\] \[(QK^t)V: (m, 512)\]즉 다음과 같이 인코더와 디코더의 sequence size가 다르더라도 attention은 올바른 차원을 가지고 진행됩니다.
임베딩 후 positonal encoding을 더하기 전에 왜 $\sqrt{d_{model}}$을 인풋에 곱해주는가?
논문의 내용중 “In the embedding layers, we multiply those weights by $\sqrt{d_{model}}$.”라는 부분의 동기가 잘 이해가 되지 않았습니다. Attention 메커니즘 쪽에서 $\sqrt{d_{model}}$로 나누는 건 워낙 눈에 띄니까 알아차리기 쉬운데, positional encoding을 더하기 전에 $\sqrt{d_{model}}$를 곱해주는 것의 동기가 의아했습니다. 찾아보다보니 하나의 가설이 가장 그럴듯 했는데, 이 글 속 답변의 내용처럼 임베딩 가중치는 모두 표준정규분포를 따르게 초기화가 되어서 그냥 사용하면 -1~1 사이의 값을 가지는 positional encoding 값에 너무 영향을 많이 받는다는 내용이었습니다. 그렇기에 의도적으로 임베딩 벡터의 가중치를 positional encoding에 비해 높여준 것이라고 이해할 수 있었습니다.
이 외에도 이 논문에 대한 흥미로운 질문이 있다면 언제든지 댓글로 남겨주세요!
동일한 영어 포스트
Attention is all you need - Fully grasping the legendary paper
참고한 글, 문서
- https://arxiv.org/abs/1706.03762
- “밑바닥부터 시작하는 딥러닝”, 사이토 고키. 한빛미디어 2017
- https://pytorch.org/tutorials/beginner/basics/intro.html
- https://www.youtube.com/watch?v=zxagGtF9MeU&list=PLblh5JKOoLUIxGDQs4LFFD–41Vzf-ME1
- https://www.youtube.com/watch?v=aircAruvnKk&list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi
- https://jalammar.github.io/illustrated-transformer/
- https://www.youtube.com/watch?v=IGu7ivuy1Ag
- https://towardsdatascience.com/transformer-networks-a-mathematical-explanation-why-scaling-the-dot-products-leads-to-more-stable-414f87391500
- https://stats.stackexchange.com/questions/534618/why-are-the-embeddings-of-tokens-multiplied-by-sqrt-d-note-not-divided-by-s
아직 부족한 점이 많아 미흡하거나 틀린 내용이 있으면 댓글로 알려주시면 감사하겠습니다. 제안이나 질문도 언제든지 남겨주세요! 🙇♂️